Simpson's Paradox Explains the World

It’s everywhere you look

Genuine paradoxes have unstable truth values. The American Philosophical Association used to sell a t-shirt that read on the front “The sentence on the back of this shirt is false” and on the back it read “The sentence on the front of this shirt is true.” The pair of sentences is unstable because as soon as you say that one of them is true, a second later you realize that it must actually be false. But if it is false, then it turns out true again. Aaaaah! Paradoxes are disturbing, and there’s a whole bunch of these things, accompanied by some fairly wacky theories that try to solve them.

Simpson’s Paradox is not a genuine paradox in the above sense. But it is pretty unexpected nevertheless, and leads to some results that one might naively think wouldn’t happen. However, as soon as I understood how it worked I started seeing Simpson’s Paradox everywhere and it gave me a way to address a bunch of otherwise puzzling questions.

I think of it in set-theory terms. Simpson’s Paradox arises when you can partition a set into proper subsets, most of which have a property which is opposite to the superset. The encyclopedia definition is “Simpson’s Paradox is a statistical phenomenon where an association between two variables in a population emerges, disappears or reverses when the population is divided into subpopulations.” I think we’re basically saying the same thing. Here’s some examples.

Examples

Sports. In the 2019 Wimbledon men’s final, Novak Djokovic beat Roger Federer 7–6 (tiebreaker 7-5), 1–6, 7–6 (tiebreaker 7-4), 4–6, 13–12 (tiebreaker 7-3). However, Federer won more points (218 to Djokovic’s 204) and he won more games (36 to Djokovic’s 32). Yet Federer still lost the match. Why didn’t he win? Because in tennis, games are partitioned into (tennis) sets, and in men’s professional tennis it takes three of five sets to win the match. That’s what Djokovic achieved.

Voting. In the 2016 US presidential election, Donald Trump beat Hillary Clinton, even though Clinton got almost 3 million more votes. The popular vote is partitioned by the Electoral College, as games in tennis matches are partitioned by sets, and Trump won most of the Electoral College votes. The Electoral College has paid off for Republicans: all US Presidents who failed to get the popular vote were Republicans (J. Q. Adams in 1824, Hayes in 1876, B. Harrison in 1888, G. W. Bush in 2000, and Trump in 2016). Obviously supporters of Jackson, Tilden, Cleveland, Gore, and H. Clinton complained that the Electoral College thwarted the will of the people and that their favored candidate should have been properly declared the victor.

Gerrymandering. Generally this expression is used when it comes to carving up voting districts, and goes back to Elbridge Gerry, the Governor of Massachusetts who first did this in 1812. Again, it is a way of partitioning data, in this case, individual votes, so that a favored partisan candidate wins. In practical terms, it’s when district boundaries are drawn around enclaves of, say, Republicans so that Republican nominees are guaranteed to win the district. In the example below the “voting districts” are drawn up to ensure Green’s win, even though Black got most of the votes, much as Federer lost at Wimbledon despite winning most of the games.

Literacy: Alex Tabarrok offers this nice example:

Between 1992 and 2003 US literacy rates fell dramatically within every single educational category but the aggregate literacy rate didn’t budge. A great example of Simpson’s Paradox! The easiest way to see how this is possible is just to imagine that no one’s literacy level changes but everyone moves up an educational category. The result is zero increase in literacy but falling literacy rates in each category.

The original data for this claim is here.

Climate change: It is entirely possible for most months out of the year to be colder than average, while the year itself is hotter than average. So by focusing on the daily temperature or even the monthly temperature, we’ll miss the true trend over the year. In the following chart eight of 12 months are colder than the historical average but over all the year is seven degrees warmer than average. Obviously this idea could be expanded: most years could be colder but the decade itself is warmer.

Utilitarianism: Utilitarianism, in its most basic form, holds that of the range of possible actions you might perform at a given time, you are morally obligated to do the one that has the best consequences. Consequences are all that matter for the moral evaluation of action, and (classically) those consequences are measured in terms of pleasure and pain. We should be maximizing the world’s happiness with our actions and minimizing its pain.

Unfortunately, under utilitarianism we may be obligated to make every living person less happy, because it will increase the total global amount of happiness.¹ Thanks a lot, Simpson’s Paradox. Consider the following two scenarios.

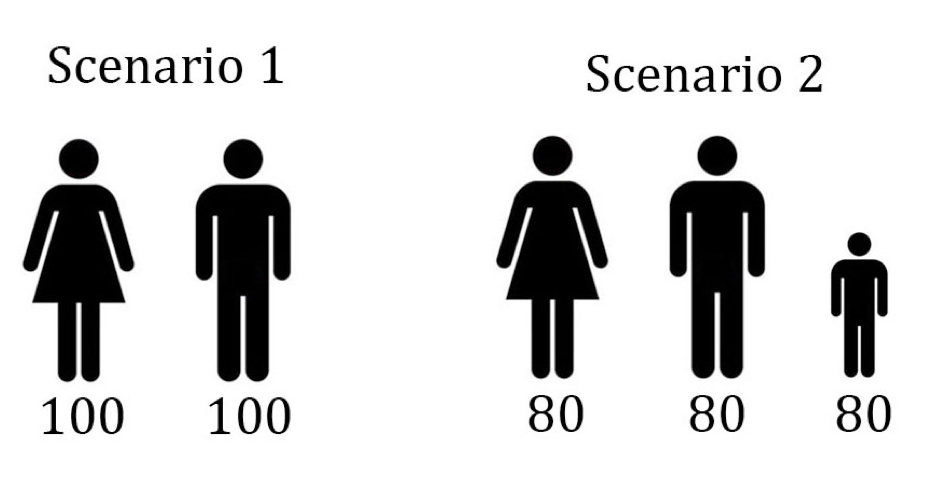
In Scenario 1, imagine that there are two people alone on a desert island. It isn’t a paradise; there’s limited food, water, and shelter and the two people have to struggle for survival. Suppose that nonetheless they are reasonably happy. Let’s say that each person has a total of 100 units of happiness at the end of their life. The numbers don’t matter; they’re just placeholders to indicate relative values. Now, suppose that the couple is considering having a child, and creating Scenario 2. In this condition each adult is a bit less happy; they have to work that much harder to provide for their child on an island of scarce resources. Still, the child has a fairly happy life, and the parents, while less happy, are still in the positive numbers for lifetime happiness.

Which is the morally preferable world according to utilitarianism? The answer is Scenario 2, because it is an overall happier world than Scenario 1, totaling 240 happiness units to 200. In this case, the couple on the desert island is morally obligated to create more people, even though it makes everyone there less happy. That is deeply mysterious. The desert island scenario, while somewhat abstract, is not that far removed from reality. It is not hard to imagine that the entire planet is like the desert island, and that we might under utilitarianism be obligated to keep increasing the human population until we reach a tipping point, even if by doing so we make every living person less happy.

Government: Here Simpson’s Paradox shows up when a majority of government programs are supported by a majority of voters, but it is also the case that more voters want to shrink the government. Matthew Yglesias comes close to seeing this when he writes,

If Social Security didn’t exist, conservatives would obviously hate the idea of it. We’d be talking about a gigantic increase in federal spending financed by a broad-based tax increase with the explicit intention of reducing people’s incentive to work. It’s popular, in large part, because it already exists. I don’t totally understand how it is that decidedly conservative people who routinely vote for Republican Party candidates and complain about government spending have reconciled themselves to the apparent contradiction, but they clearly have.

And this is part of a larger phenomenon that everyone seemingly used to be aware of, where the public tends to espouse conservative ideological concepts but then also agrees with lots of specific liberal positions.

Focusing on the parts yields a different judgment about what people want from what focusing on the whole does. They aren’t inconsistent: it’s just that different coalitions support different programs, and each is a simple majority of voters.

Pleasure. Domain experts get more pleasure from high-end experiences than newbies who are less able to appreciate fine nuances. The downside is that once you’re used to the best, the entry-level becomes insipid and boring. Conversely, novices are happier with lower-quality experiences than those snooty elites. If you are new to video games, novels, chocolate, automobiles, skateboards, pizza, smartphones, whatever, just about anything seems good, if not amazing. A comparison between the experts and novices gives rise to Simpson’s Paradox results.

Suppose that a beer expert and a beer novice decide to drink a brew together every night for a month. Their financial resources are limited, so they cannot afford artisanal craft beer every night. Most nights they drink corporate mass-produced lager, but once in a while they splurge and drink the top-shelf stuff. Expert gets very little pleasure on the nights when they drink Yuengling or Budweiser and very great pleasure the evenings they share a Bruery Black Tuesday or a Trappistes Rochefort 10. Novice likes Yuengling and Bud just fine, although he is not a complete idiot and enjoys Rochefort 10 a bit more. Their month of tasting can be presented graphically, with the days on the x axis and the units of pleasure on the y axis.

Novice is happier than Expert nearly every day. But when it is added all up, Expert is happier than Novice for whole month.

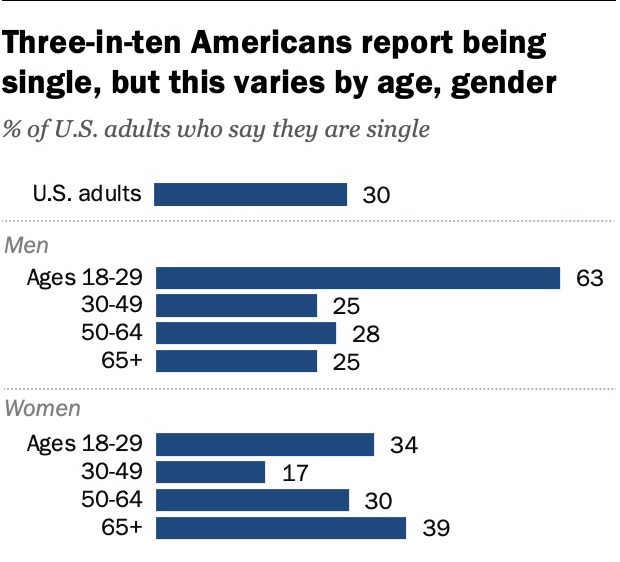
Dating: The number of men and women is the same, or it’s close enough for government work. Setting aside the few polygamous or polyandrous relationships, the number of men in a committed relationship should be exactly the same as the number of women in one: everyone pairs off and do-si-do your partner. Perhaps the Simpson’s Paradox results aren’t quite as striking here, but look at this data.

Source

Men between the ages of 18-50 are no doubt frustrated by the lack of available women in their age group. Where are all the single women? How can they be all taken when so many men are not? Women get to be pretty choosy until they are senior citizens, then the men finally have an advantage (presumably because their rivals are dying off).

Analysis

So what should we looking at? The stats about the group? The individuals? Is there some optimal way of partitioning the data? I wish it were that simple.

In some of the examples above, it is an open question about how the basic facts should be grouped together. For example, a Federer fan might reasonably argue that Federer outplayed Djokovic at Wimbledon in 2019. After all, he won most of the points and most of the games. If winning a match is supposed to reflect who the best player was, then Federer should have been declared the victor. There’s something capricious about dividing the points and games up in such a way that Djokovic came out on top.

The obvious response from the Djokovic camp is, of course, “well, those are just the rules of tennis. Deal with it.” However, the rules of tennis are conventional, and as with many other sports they might change and evolve over time. In fact, they have. Still, it is possible for all players to agree about which shots were in and which ones out (the ground-level facts) but continue to disagree about which player performed the best.

All games are unnecessary actions performed in accordance with unnecessary rules. The rules are just invented to make the game more fun, exciting, or entertaining. There’s no optimal list of rules, or some kind of Perfect Rulebook for tennis, so we can just keep debating Federer vs. Djokokic as long as we like.

Other ways of grouping data are obviously terrible, like gerrymandering. For example,

That ain’t right. Can’t we just tesselate each state with compact polygons and make those congressional districts? Likewise for climate change: what matters there is longer-term trends, not what’s happening month-to-month.

In other cases there are better and worse ways of doing things, but no best way. Voting, for example. There are lots of different voting methods: first-past-the-post, Borda counting, ranked-choice, etc. Every possible voting scheme is subject to strategic voting; i.e. it can be gamed.² But it is also the case that some are more easily gamed than others; some voting methods are better than others. Kenneth Arrow famously proved that no possible voting scheme can meet certain plausible constraints for being an ideal scheme. For that he won the Nobel prize. In short, the Electoral College might be stupid, but nothing is perfect.

With the drinking beer example it’s not even clear that there are better and worse ways of doing things. Should we become aficionados of high-end pleasures (as John Stuart Mill recommended), even if they may be rare or expensive, or should we remain novices who are fairly happy with whatever is on tap? There are trade offs with both options and neither looks obviously better to me.

Sometimes the lesson is that we just need to be more aware of what perspective we’re taking—are we focused on the parts (like government programs) and ignoring the whole? Are we doing the reverse? What seems more appealing in that example might just depend on the point of view we’re adopting to consider the data.

For me, having Simpson’s Paradox in my tool belt helps me understand both how certain weird results come about, but also how people might agree about the fundamental facts but come to very different conclusions about what they mean. In our partisan times that’s a handy thing to have.

1. This is a form of Derek Parfit’s famous Repugnant Conclusion, but the basic idea goes back to Henry Sidgwick. Nobody else seems to have noticed that it’s Simpson’s Paradox rearing its head again.

2. This is the Gibbard-Sattherthwaite theorem.